Number sets
A set is a collection of objects. These objects, called the members or elements of the set, are enclosed in braces {...} and separated by commas.
A set can be described in words: A = { the first four whole numbers}
or by listing each member: A = {0, 1, 2, 3}.
The numbers we use can be chosen from several sets.
- The set of natural numbers. These are the counting numbers.N = {1, 2, 3, 4, ...}
-
The set of whole numbers. These are the counting numbers plus zero.
W = {0, 1, 2, 3, ...}
-
The set of integers. These are the negative and positive numbers.
I = {... -2, -1, 0, 1, 2, 3,...}
Numbers from these number sets can be shown on number lines.
This number line shows five integers. The further to the LEFT a number lies, the SMALLER it is.
From the number line it can be seen that:
| -6 < -4 | negative six is LESS THAN negative four. |
| 7 > 0 | positive seven is GREATER THAN zero. |
| -4 < 2 | negative four is LESS THAN positive two. |
Other sets include rational numbers, irrational numbers, real numbers and complex numbers.
Calculations with Integers
The integers are the positive and negative numbers and zero. Just like any other numbers they can be added, subtracted, multiplied and divided.
Adding Integers
Use a number line when adding and subtracting integers. The first integer is the starting point on the number line.
When adding a positive integer, move to the right.
e.g. 4 + 2 = 6
When adding a negative integer, move to the left.
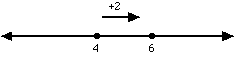
Subtracting Integers
When subtracting a positive integer, move to the left.
e.g. 4 − 2 = 2
When subtracting a negative integer, move to the right
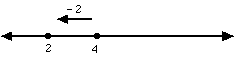
e.g. 4 − -2 = 6
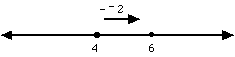
Multiplying and Dividing Integers
The rule is the same for both multiplying and dividing two integers.
If the signs of the two integers are the same, the answer is positive.
If the signs of the two integers are different, the answer is negative.
The table illustrates these rules:
Examples:
For practice with integer calculations − 
|
Applications
|
|||
|
a
|
The price of a company's shares rose 23 cents on Monday, and fell 29 cents on Tuesday. What was the rise or fall of the share's price over the two days? |
Price change = 23 + -29 The share price fell 6 cents over the two days. |
|
|
b
|
At the beginning of the year 32 students joined Red Bay Primary School. During the year 12 students left and at the end of the year another 21 left. What was the total gain or loss of students over the year? |
Change in number of students There was a loss of one student over the year. |
|
|
c
|
Fiona's rabbit lost 18 grams in weight. Then it gained 22 grams. What was the total loss or gain in weight? |
 |
Weight change = -18 + 22 There was a weight gain of 4 grams. |
