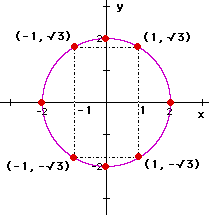Other Types of Graphs

Graphing_hand.jpgAs well as straight line coordinate graphs there are many functions whose graphs have different shapes.
These functions will become more important in future years.
Below are some examples of the different types of functions and their graphs are sketched by plotting points.

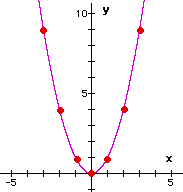
Parabolas

A parabola is a curved graph produced by a quadratic function, one which contains a "squared" x-term.

y = x2

x
y
Coordinates
-3
(-3)2 = 9
(-3, 9)
-2
(-2)2 = 4
(-2, 4)
-1
(-1)2 =1
(-1, 1)
0
(0)2 = 0
(0, 0)
1
(1)2 = 1
(1, 1)
2
(2)2 = 4
(2, 4)
3
(3)2 = 9
(3, 9)

Y9_Other_Types_of_Graphs_01.gif

This shape is called a parabola.

 

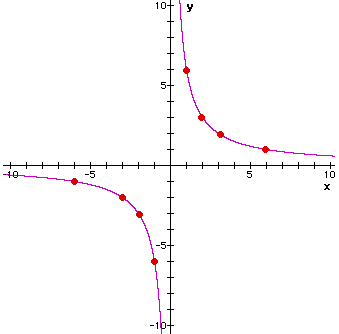
Hyperbolas

The equation of a hyperbola contains an x-term and a y-term multiplied together. The general equation is xy = c, where c is a constant.

xy = 6

x
y
Coordinates
-3
-2
(-3, 2)
-2
-3
(-2, -3)
-1
-6
(-1, -6)
0
no number possible
undefined
1
6
(1, 6)
2
3
(2, 3)
3
2
(3, 2)

x multiplied by y has to always be 6.

The lines x = 0 and y = 0 on the graph are called asymptotes.

They are not crossed by the curves.

Y9_Other_Types_of_Graph_02.gif

This shape is called a hyperbola.

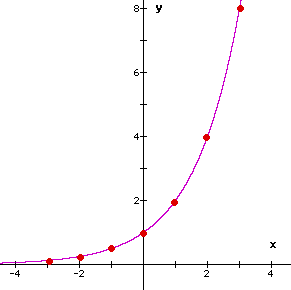
Growth Curves

The equation of a growth curve has a power of x. The general equation is y = ax, where a is a constant.

y = 2x

x
y
Coordinates
-3
0.125
(-3, 0.125)
-2
0.25
(-2, 0.25)
-1
0.5
(-1, 0.5)
0
1
(0, 1)
1
2
(1, 2)
2
4
(2, 4)
3
8
(3, 8)

 

Check these results using the Y9_Other_Types_of_Graph_03.gif button on a calculator.

The x-axis is an asymptote.

 

Y9_Other_Types_of_Graph_04.gif

This shape is called a growth curve or an exponential function.

Circles

The equation of a circle contains an x2 and a y2 term. The general equation is x2 + y2 = r2, where r is the radius.

x2 + y2 = 4

x
x2
y2
y
Coordinates
-2
4
0
0
(-2, 0)
-1
1
3
-√3 or √3
(-1, √3) and (-1, √3)
0
0
4
2 or -2
(0, -2) and (0, 2)
1
1
3
-√3 or √3
(1, √3) and (1,√3)
2
4
0
0
(2, 0)

The middle terms above, in red, have to always add to 4.

Y9_Other_Types_of_Graph_05.gif

This shape is called a circle.