BestMaths Online

Simplifying Expressions

In algebra, letters are used to stand for numbers.

The letters are often called variables or pronumerals.

It is necessary to be able to add, subtract, multipy and divide algebraic terms.

An algebraic term can be made up of coefficient, variables and exponents.
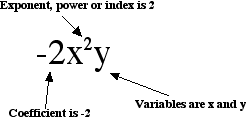Like terms have the same variables and exponents.	e.g. { 2a, 4a, -6a } are like terms. a is common to all.   { x, 3a2, 6 } are unlike terms.  There is no common term.
An algebraic expression is a group of terms.	e.g. 4x + 3y is an expression.

 

Addition and Subtraction

An expression involving addition and subtraction can be simplified only if it contains like terms.

The like terms are collected together and then added or subtracted.

Multiplying

3xy means "3 multiplied by x multiplied by y ".

In terms of this type the number comes first and the variables are usually placed in alphabetical order.

e.g. 3q × 4p = 12pq

5c × 3e × 2d = 30cde

Note that numbers are multiplied first and letters (variables) are placed in alphabetical order.

Dividing

^8xy⁄_4x means " 8xy divided by 4x ".

This type of expression is simplified by cancelling.

e.g. 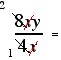 2y

Note Cancelling can only be done between numbers or letters on the top line and numbers or letters on the bottom line.

Words into Symbols

Many maths problems are written in words and these words often have to be changed into algebraic expressions.