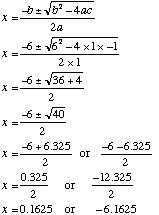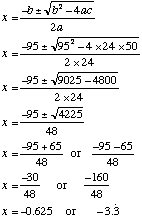Quadratic equations have one variable and the highest exponent is 2.
Quadratic equations can have zero, one or two solutions.
There are four methods for solving quadratic equations.
By factorising.
Rearrange the equation so that all of the terms are on one side of the equation. Then factorise.
The method depends on the fact that if two factors multiplied together are equal to zero, then either one or both of them must be equal to zero.
|
Solve: |
|
|
(a) x2 − 4x − 5 = 0 |
Factorise to (x − 5)(x + 1) = 0 Either: x − 5 = 0 or x + 1 = 0 x = 5 or x = -1 |
|
(b) (2x − 3)(x + 4) = 0 |
Already factorised Either: 2x − 3 = 0 or x + 4 = 0 2x = 3 or x = − 4 x = 1.5 |
|
|
Factorise to 3x(x − 2) = 0 Either: 3x = 0 or x − 2 = 0 x = 0 or x = 2 |
|
(d) (x − 4)2 = 0
|
Already factorised (x − 4)(x − 4) = 0 Either: x − 4 = 0 or x − 4 = 0 x = 4 |
By taking the square root.
Take the square root of both sides of the equation.
Remember, if x2 = a then 
|
Solve x2 = 36
|
Take the square root of both sides. x = ± 6 |
|
Solve (x − 4)2 = 9 |
Take the square root of both sides. x − 4 = ± 3 x = 7 or 1 |
By using the Quadratic Formula
When a quadratic equation cannot be factorised at all e.g. x2 + 6x − 1 = 0 or cannot be factorised easily e.g.
then a formula called the Quadratic Formula (proof) can be used:
|
For the equation ax2 + bx + c = 0 The Quadratic Formula |
|
Example 1
|
Example 2
|
|
Solve x2 + 6x − 1 = 0 a = 1
(to 4 decimal places)
|
Solve 24x2 + 95x + 50 = 0 a = 24
|
By graphing.
The solutions for the equation are the x-intercepts of the graph of the equivalent quadratic function which is a parabola.
See Topic 20
Word Problems involving Quadratic Equations
There are a range of word problems involving quadratic equations. The basic method is to:
- read the question carefully and assign a variable to the amount that is being found.
- form a quadratic equation
- solve the quadratic equation
- write the solution to the problem
Example
Francis is 10 years older than Michael. The product of their ages is 600. What are their ages?
- Let Michael's age be x
- The equation is x(x + 10) = 600
- Solve the equation:
x(x + 10) = 600
x2 + 10x = 600
x2 + 10x − 600 = 0
(x + 30)(x − 20) = 0
x = -30 OR x = 20
- Michael cannot be -30 so he must be 20 and Francis is 10 years older at 30.
