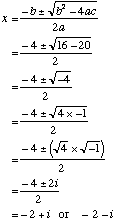BestMaths Online

Most polynomial equations can be solved with an answer from the set of real numbers.

However, there are some equations, such as x² + 1 = 0, which cannot be solved using real numbers.

This type of equation can be solved by creating one new number called i.

The definition of i is:

Use of the number i allows for the solution of a whole set of equations involving the square roots of negative numbers.

Example

Solve the quadratic equation x² + 4x + 5 = 0 using the set of real numbers plus i.

Let a = 1, b = 4 and c = 5

Using the quadratic formula:

The number system formed by the real numbers with the addition of the number i and including numbers in the form 3 + 5i is called the set of complex numbers.

Notation

The set of complex number is denoted by C.

Complex numbers are often represented by the variable z where z = a + ib

a is called the real part of the complex number z. The real part can be written Re(z).

b is called the imaginary part of the complex number z. The imaginary part can be written Im(z).

Conjugate
The conjugate of the complex number z = a + ib is  = a − ib.

The product of a complex number and its conjugate gives a real number.

e.g. (3 + 4i)(3 − 4i) = 9 -16i² = 9 − 16(-1) = 25