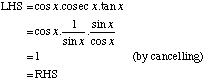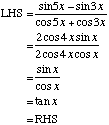An identity is an equation which is true for all values of the variable.
|
sin2x + cos2x = 1 |
Pythagorean Identities
The Pythagorean identities are worked out from the identity above sin2 x + cos2 x = 1 which was derived using Pythagoras' Theorem.
Divide each term in sin2 x + cos2 x = 1 by sin2 x
This identity is given in the tables for exams but should be memorised, if possible:
|
1 + cot2 x = cosec2 x
|
Divide each term in sin2 x + cos2 x = 1 by cos 2 x
This identity is given in the tables for exams but should be memorised, if possible:
|
cot2 x + 1 = sec2 x
|
The above identities plus the other angle formulae can now be used to help solve equations and other more complicated identities.
Proving Identities
Identities are proven in a different way to equations.
Usually one side of the identity is taken, it does not matter which, although it is often obvious which one will be the easiest to manipulate. Terms on this side of the identity are then substituted and manipulated until it is equal to the other side.
It is important to set these proofs out clearly and a system using the abbreviation RHS (right hand side) and LHS (left hand side) is often used.
|
Example 1
|
Example 2(A Bursary question)
|
|
Prove the identity cos x cosec x tan x = 1 |
Prove the identity |
|
|
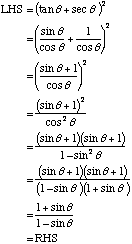 |
|
Some are easy!
|
Some are not so easy! |
Some identities use the angle formulae from Unit 43, Angle Formulae.
|
Example 3
|
Example 4
|
|
|
Prove the identity sin 3A = 3sin A − 4sin3 A |
|
|
 |
There is often more than one way to prove an identity, try to find the shortest!