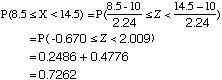Sometimes, it is difficult or impossible to use the Binomial probability formula or tables because the value of n is too large.
The binomial tables given with examinations usually only go up to n = 10.
When n has a large value binomial probability distributions begin to look more like normal probability distributions.
| Binomial, when n = 20 and p = 0.2 | Binomial, when n = 20 and p = 0.5 |
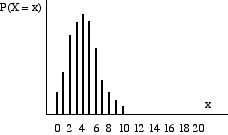 |
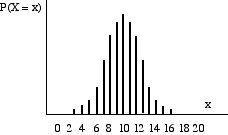 |
| Almost bell- shaped but skewed. | Bell − shaped and symmetrical |
From the two line graphs, it can be seen that for large values of n with p close to 0.5 the normal distribution can be used instead of the binomial. If q = 1 − p, then a good test is to say that if both np ≥ 5 and nq ≥ 5 then the normal can be used.
Note that because binomial values are discrete and normal values are continuous a continuity correction is necessary.
The values of the mean and standard deviation needed for the normal distribution are μ = np and σ = √(npq)
To summarise:
|
For large values of n with p close to 0.5 the normal distribution approximates the binomial distribution
|
|
| Test |
np ≥ 5 |
| New parameters |
μ = np σ = √(npq) |
Example
When 20 coins are tossed, what is the probability that between 9 and 14 heads, inclusive, will result?
Solution
This is a binomial problem with n = 20 and p = 0.5. Most tables do not go to 20, and to use the binomial formula would be a lengthy process, so consider the normal approximation.
Step 1 Test to see if this is appropriate.
np = 20 × 0.5 = 10 and nq = 20 × 0.5 = 10. Both are greater than 5.
Step 2 Find the new parameters.
μ = np = 20 × 0.5 = 10
σ = √(npq) = √(20 × 0.5 × 0.5) = 2.24 (to 3 s.f.)Step 3 Apply continuity correction.
Let X be the number of heads thrown
P( 9 < X < 14) becomes P(8.5 ≥ X < 14.5)Step 4 Use normal tables to solve problem.
The probability that between 9 and 14 heads will result is 0.7262