Simultaneous equations are sets of two or more equations with solutions which must be correct for the variables in each equation.
Simultaneous equations can contain any number of variables but are only easily solvable if there are the same number of variables as there are equations.
The Bursary Statistic prescription covers groups of two simultaneous equations with two variables and three equations with three variables. The functions used are linear (straight line) systems.
Two Simultaneous Equations
Systems with two simultaneous equations will already been studied in earlier years.
Two methods of solution will be focussed on in this topic, the substitution method and the elimination method.
|
Substitution method
|
Elimination method
|
|
If one of the equations has a variable alone as the subject, it can be directly substituted into the other equation. |
If the coefficients of either x or y are the same, or can easily be made the same, then either the x or the y term can be eliminated by adding or subtracting the two equations, |
|
y = 3x + 4 ...................A x + y = 12 .......................B Substitute 3x + 4 for y into equationB 4x + 4 = 12 4x = 8 x = 2 Substitute x = 2 into equation B y = 10 |
4x + 3y = 24 ...................A 3x − y = 5 ..........................B Multiply equation B by 3 9x − 3y = 15 ..................C Add equation A to equation C 4x + 3y = 24 Substitute x = 3 into equation A 12 + 3y = 24 3y = 12 y = 4 |
| The solution is (2, 10) | The solution is (3, 4) |
Three Simultaneous Equations
With systems of three equations with three variables there are several methods of solution.
This topic will use the elimination method. The steps are:
- Take two of the equations and eliminate one of the variables (e.g. equations 1 and 2).
- Take two more of the equations and eliminate the same variable (e.g. equations 2 and 3)
- Use the two new equations found earlier and elinimate a further variable.
- Use substitution to find the values of the other two variables.
Example
Solve the simultaneous equations:
|
Label each equation.
|
4p − 5q +3t
|
=
|
7 | .......A |
|
3p + 5q − 4t
|
=
|
19 | .......B | |
|
2p + q − 3t
|
=
|
5 | ........C | |
|
Take equations A and B
|
||||
|
4p − 5q +3t
|
=
|
7 | .......A | |
|
3p + 5q − 4t
|
=
|
19 | .......B | |
|
Add A and B
|
7p − t
|
=
|
26 | .......D |
|
Take equations B and C
|
||||
|
3p + 5q − 4t
|
=
|
19 | .......B | |
|
x C by 5
|
10p +5q − 15t
|
=
|
25 | .......C |
|
Subtract B from C
|
7p − 11t
|
=
|
6 | ........E |
|
Take equations D and E
|
||||
|
7p − t
|
=
|
26 | .......D | |
|
7p − 11t
|
=
|
6 | ........E | |
|
Subtract E from D
|
10t
|
=
|
20 | |
|
t
|
=
|
2 | ||
|
Substitute t = 2 into E
|
7p − 22
|
=
|
6 | |
|
7p
|
=
|
28 | ||
|
p
|
=
|
4 | ||
|
Substitute t = 2and p = 4 into A
|
16 − 5q + 6
|
=
|
7 | |
|
q
|
=
|
3 |
Solution set is {p, q, t} = {4, 3, 2}
Consistency and Uniqueness of Solutions
Two equations
For systems of two equations:
|
Lines Intersect
|
Lines are parallel
|
Same line − equations in different form
|
 |
 |
 |
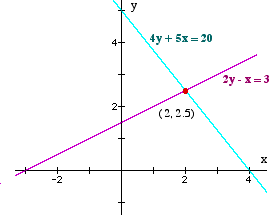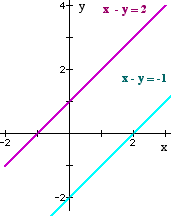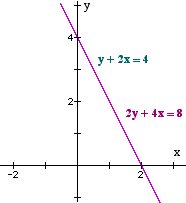| One solution − unique |
No solution − inconsistent (When working leads to 0 = 4 or similar.) |
Many solutions − dependent (When working leads to 0 = 0 or similar.) |
Three equations
For systems of three equations, equations in three variables can be represented by a plane (the three green lines are the perpendicular x, y and z axes.):
|
Planes Intersect
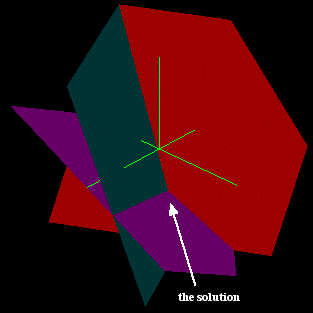
e.g. -x + 2y − z = 1 x − y + 2z = -2 2x + y − z = 2 |
Click here to see rotation of graph |
One solution unique
|
|
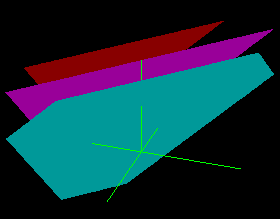
e.g. x − y + z = 1 x − y + z = 2 x − y + z = 3 |
Click here to see rotation of graph |
No solution inconsistent (When working leads to 0 = 4 or similar.) |
|
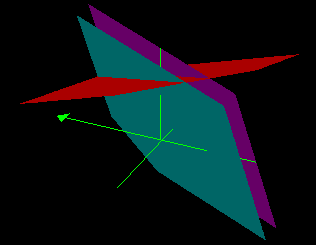
Two planes are parallel, other is not e.g. 2x − y + z = 1 2x − y + z = 2 x + y + 3z = 4 |
Click here to see rotation of graph |
No solution inconsistent (When working leads to 0 = 4 or similar.) |
|
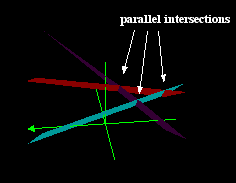
Lines where pairs of planes intersect are parallel. e.g. 2x + y + 2z = 3 2x − 2y + 2z = 4 4x − y + 4z = 6 |
Click here to see rotation of graph |
No solution inconsistent (When working leads to 0 = 4 or similar.) |
|
All three planes intersect along the same line. e.g. 2x + y + 2z = 3 2x − 2y + 2z = 4 4x − y + 4z = 7
|
Infinite number of solutions along the common line. dependent (when working leads to 0 = 0 or similar.) |
Applications of Simultaneous Equations
Word problems involving simultaneous equations can be long and appear daunting. The first step is to assign variables to the unknowns in the question. Then formulate the two or three equations needed. Finally solve the equations. Sounds easy!
Example (Bursary Question)
The Health Club serves a special meal consisting of three kinds of food, A, B and C.
Each unit of food A has 20 g of carbohydrate, 2 g of fat and 4 g of protein.
Each unit of food B has 5 g of carbohydrate, 1 g of fat and 2 g of protein.
Each unit of food C has 80 g of carbohydrate, 3 g of fat and 8 g of protein.
The dietitian designs the special meal so that it contains 140 g of carbohydrate, 11 g of fat and 24 g of protein. Let a, b and c be the number of units of food A, B and C (respectively) used in the special meal.
Set up a system of 3 simultaneous equations relating a, b and c. Do not solve the equations.
Solution
20a + 5b + 80 c = 140
2a +b + 3c = 11
4a + 2b + 8c = 24
If required, these simultaneous equations could be solved using the elimination method demonstrated above to find the values of a, b and c.
